1. Persamaan Kuadrat
Bentuk umum persamaan kuadrat dalam variabel x adalah
dengan 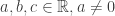
 .
.
2. Penyelesaian Persamaan Kuadrat
Penggunaan Diskriminan D
Diskriminan dari persamaan kuadrat adalah  .
.
Untuk menentukan jenis akar.
Jenis-Jenis Akar Persamaan Kuadrat
- D > 0, berarti persamaan kuadrat memiliki 2 akar real dan berbeda.
- D = 0, berarti persamaan kuadrat memilik 2 kar real dan sama/kembar.
- D < 0, berarti persamaan kuadrat memiliki 2 akar tidak real(imajiner) dan berbeda.
3. Rumus Jumlah dan Hasil Kali Akar-Akar Persamaan Kuadrat
- Jumlah :
.
- Selisih :
.
- Kali :
.
4. Persamaan Kuadrat Baru dengan Akar-Akar  dan
dan  .
.
Fungsi Kuadrat
Adalah suatu fungsi yang berupa  .
.
Beberapa hal yang perlu diketahui berkaitan dengan persamaan dan fungsi kuadrat adalah:
- Jika
, kurva terbuka ke atas.
- Jika
, kurva terbuka ke bawah.
- Jika
, kurva memotong sumbu x di dua titik yang berbeda.
- Jika
, kurva menyinggung sumbu x.
- Jika
, kurva tidak memotong dan tidak menyinggung sumbu x.
5.1 Fungsi kuadrat jika grafiknya menyinggung sumbu X di titik  dan melalui sebuah titik tertentu, maka persamaan fungsi kuadratnya adalah
dan melalui sebuah titik tertentu, maka persamaan fungsi kuadratnya adalah
5.2 Fungsi kuadrat jika grafiknya memotong sumbu X di titik  adalah
adalah
5.3 Fungsi kuadrat jika grafiknya melalui titik puncak/balik/ekstrim  dan melalui sebuah titik tertentu, maka persamaan fungsi kuadratnya adalah
dan melalui sebuah titik tertentu, maka persamaan fungsi kuadratnya adalah
Pertidaksamaan Kuadrat
Bentuk umum:
1. Persamaan kuadrat  mempunyai akar
mempunyai akar  dan
dan  . Jika
. Jika  memiliki akar
memiliki akar  dan
dan  , maka nilai dari
, maka nilai dari  adalah ….
adalah ….
Jawab:
2. Diketahui persamaan kuadrat  memiliki akar yang berlawanan
memiliki akar yang berlawanan 
, tentukanlah dan
dan 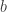 .
.
, tentukanlah
Jawab:
Diketahui bahwa
3. Tentukanlah semua nilai  sehingga persamaan
sehingga persamaan  memiliki tepat dua solusi real untuk
memiliki tepat dua solusi real untuk  .
.
Jawab:
Kita ambil yang  .
.
Catatan:
Jawaban ini sekaligus koreksi jawaban di ebook Materi dan Contoh Soal Olimpiade Matematika MA/SMA pada soal yang sama. Apabila pembaca sekalian masih menemukan ada kesalahan, saya dengan senang hati menerima masukan dan sekaligus solusi yang paling tepat dari pembaca sekalian untuk pencerahan kepada saya khususnya dan pemirsa pada umumnya).
4. Jika 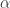 dan
dan 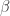 adalah akar-akar dari persamaan
adalah akar-akar dari persamaan  , maka tentukanlah nilai berikut tanpa menyelesaikan persamaannya terlebih dahulu
, maka tentukanlah nilai berikut tanpa menyelesaikan persamaannya terlebih dahulu
Jawab:
Diketahui persamaan
A. Bentuk Umum dan Sifat Parabola
Kurva fungsi kuadrat y = f( x ) = ax2 + bx + c, a tidak sama dengan nol ( 0 ) berbentuk parabola.
Jika nilai a > 0 maka parabola terbuka ke atas dan mempunyai nilai ekstrem minimum
Jika nilai a < 0 maka parabola terbuka ke bawah dan mempunyai nilai ekstrem maksimum
Koordinat titik puncak / titik ekstrem / titik stationer / titik balik parabola adalah ( Xp , Yp ) dengan :
Xp = absis ( x ) titik puncak = sumbu simetri = absis ( x ) saat mencapai nilai maksimum/minimum
Yp = ordinat ( y ) titik puncak = nilai ekstrem/nilai stationer/nilai maksimum/nilai minimum
B. Sketsa Grafik Fungsi Kuadrat / Parabola
Langkah-langkah dalam membuat sketsa grafik fungsi kuadrat/parabola ( y = ax2 + bx + c) :
1. menentukan titik potong grafik dengan sumbu x → y = 0
kemudian difaktorkan sehingga diperoleh akar-akarnya yaitu x1 dan x2 . jika kesusahan dalam memfaktorkan coba di cek dulu nilai D nya….
jika D < 0 maka fungsi tersebut memang tidak mempunyai akar-akar persamaan fungsi kuadrat sehingga sketsa grafik fungsi kuadrat tidak memotong sumbu x
jika D > 0 maka fungsi tersebut mempunyai akar-akar persamaan fungsi kuadrat namun kita kesulitan dalam menentukannya… bisa jadi karena angkanya yang susah difaktorkan atau faktornya dalam bentuk desimal. Akar-akarnya dapat kita cari dengan rumus abc :
 setelah kita mendapatkan nilai x1 dan x2 maka titik potong grafik fungsi kuadrat dengan sumbu x :
setelah kita mendapatkan nilai x1 dan x2 maka titik potong grafik fungsi kuadrat dengan sumbu x :( x1 , 0 ) dan ( x2 , 0 )
2. menentukan titik potong grafik dengan sumbu y → x = 0karena x = 0 maka y = c dan titik potong dengan sumbu y = ( 0 , c )
3. menentukan sumbu simetri ( xp ) dan titik ekstrem ( yp )
dari penentuan sumbu simetri ( xp ) dan nilai eksterm ( yp ) diperoleh titik puncak grafik fungsi kuadrat/parabola : ( Xp , Yp )
Posisi grafik fungsi kuadrat/parabola terhadap sumbu x
mengulang pembahasan mengenai titik potong sumbu x → y = 0 ada 3 kemungkinan :
mengulang pembahasan mengenai titik potong sumbu x → y = 0 ada 3 kemungkinan :
D > 0 → grafik fungsi kuadrat memotong sumbu x di dua titik
D = 0 → grafik fungsi kuadrat menyinggung sumbu x di satu titik
D < 0 → grafik fungsi kuadrat tidak memotong sumbu x
D = 0 → grafik fungsi kuadrat menyinggung sumbu x di satu titik
D < 0 → grafik fungsi kuadrat tidak memotong sumbu x
dengan menggabungkan dengan nilai a nya dapat dibuat sketsa grafik fungsi kuadrat/parabola :
C. Persamaan Fungsi Kuadrat / Parabola
1. Diketahui tiga titik sembarang
Rumus : y = ax2 + bx + c
nilai a, b dan c ditentukan dengan eliminasi.
2. Parabola memotong sumbu x di dua titik ( x1 , 0 )dan ( x2 , 0 ) dan melalui satu titik sembarang.
Rumus : y = a ( x – x1 ).( x – x2 )
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
3. Parabola menyinggung sumbu x di satu titik ( x1 , 0 ) dan melalui satu titik sembarang.
Rumus : y = a ( x – x1 )2
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
4. Parabola melalui titik puncak ( xp , yp ) dan melalui satu titik sembarang.
Rumus : y = a ( x – xp )2 + yp
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
D. Hubungan Kurva Persamaan Kuadrat / Parabola dan Persamaan Garis Lurus











Tidak ada komentar:
Posting Komentar